Pre-training Small LMs
Published:
TLDR: A primer on how to pre-train small language models in the 1B-2B range, with a limited compute budget.
Scaling laws
Since the target model size is in the 1B-2B range, we study the scaling laws indicating the dataset size required to reach the best training efficiency.
Scaling Laws propose a framework to estimate the optimal data and model size given a compute budget. We report the results of the experiments from the Chinchilla paper.
| Parameters | FLOPs | FLOPs (Gopher unit) | Tokens |
|---|---|---|---|
| 400 Million | 1.92e+19 | 1/29,968 | 8.0 Billion |
| 1 Billion | 1.21e+20 | 1/4,761 | 20.2 Billion |
| 10 Billion | 1.23e+22 | 1/46 | 205.1 Billion |
| 67 Billion | 5.76e+23 | 1 | 1.5 Trillion |
| 175 Billion | 3.85e+24 | 6.7 | 3.7 Trillion |
| 280 Billion | 9.90e+24 | 17.2 | 5.9 Trillion |
| 520 Billion | 3.43e+25 | 59.5 | 11.0 Trillion |
| 1 Trillion | 1.27e+26 | 221.3 | 21.2 Trillion |
| 10 Trillion | 1.30e+28 | 22515.9 | 216.2 Trillion |
Estimated optimal training FLOPs and training tokens for various model sizes. For various model sizes, we show the projections from Approach 1 of how many FLOPs and training tokens would be needed to train compute-optimal models.
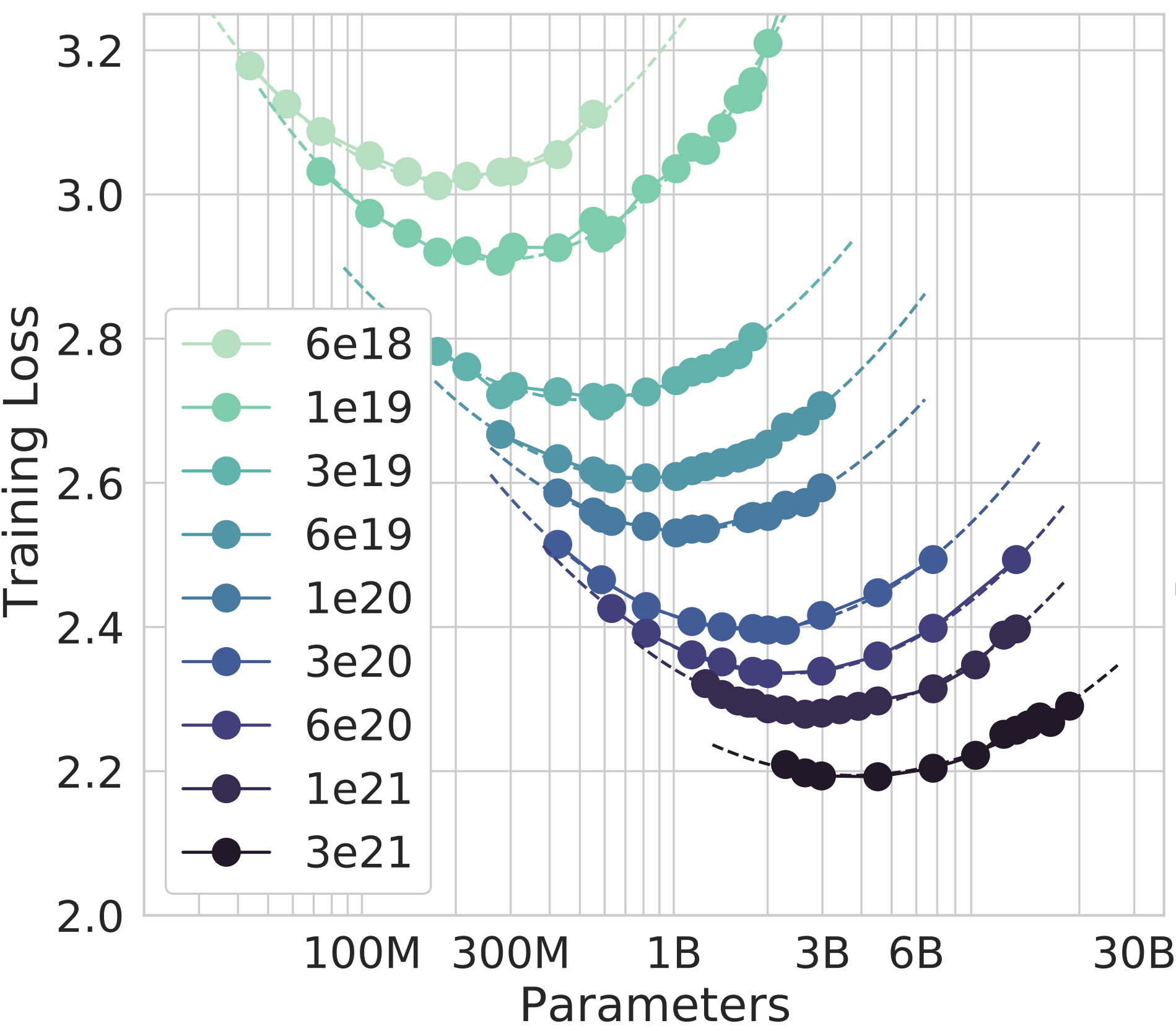
Isoflop curves showing the tradeoff between model size and loss, from Chinchilla
Reference runs
In practice, scaling laws are vastly ignored, and people pre-train for much more than the recommended data sizes to reach a better performance. We give a few examples of some pre-training efforts from different sources, and highlight the associated compute budget.
Distillation (Llama 3.2, Gemma 2)
The small-scale Llama 3.2 and Gemma 2 models were obtained via distillation from the logits of the larger models, which is not exactly pre-training from scratch.
The small Llama 3.2 models were trained on “up to 9T tokens” (for 1B and 9B). For Gemma 2: “We train Gemma 2 27B on 13T tokens of primarily-English data, the 9B model on 8T tokens, and the 2B on 2T tokens.”
Phi-3
Phi-3-mini (3.8B), was trained for 3.3T tokens (but synthetic).
SmolLM
From the Hugging Face team, joint effort with the data team (that released the FineWeb, FineWeb Edu, and FineMath datasets).
For the 1B-2B range, the dataset sizes ranges from 2T to 11T tokens, depending on the target performance.
Computing the MFU
We now try to estimate the number of GPU hours required to train such a model on a trillion-token scale dataset. We first introduce the notion of model flops utilization (MFU), that quantifies how the implementation utilizes the theoretical compute that one can get from a given hardware configuration.
The general formula for computing the efficiency of a training method with respect to the theoretical hardware maximum is (cf Annex B of the PaLM paper):
\[\eta = \frac{(6N+12LHQT)\cdot D/\tau}{P}\]where:
- \( \eta \) is the MFU (model flops utilization, between 0 and 1)
- \(P\) is the peak throughput (e.g. 312 TFLOP/s for A100)
- \(N\) is the number of parameters
- \(L, H, Q, T\) are the number of layers, the number of heads, the head dimension, and the sequence length respectively
- \(D/\tau\) is the number of tokens consumed per second
Detail of the estimation:
- For the matmuls: \(2N\) for forward, \(4N\) for backward, resulting in \(6N\).
- For the dense self-attention, \(6LH(2QT)\) FLOPs per token
As the model size and number of GPUs increases, it gets harder to reach a good MFU, especially when combining the parallelization schemes. For example, the ultra-scale playbook reaches 40% MFU for their best runs.
Estimation
The compute budget is simply obtained by multiplying the available training time by the throughput of the GPUs, scaled by the MFU.
- We give an estimate for dataset sizes between 1T and 10T tokens.
- The sequence length is set to 2,048, we do not consider sequence length warmup methods or context extension.
- The inner dimension is set to 2,304, the number of layers is set to 26 (Gemma 2 parameters).
- The MFU \( \eta \) is usually between 20% and 50%1, we set it to 35%.
- The peak flops is 312 TFLOPs for A100 (H200 have higher peak TFLOPs2).
Rewriting the formula for the MFU, we get the training time:
\[\tau = \frac{D \cdot (6N+12LHQT)}{P \cdot \eta}\]We can now compute the training time for a 1B and 2B model, with the following parameters:
| Model Size | 1T tokens | 2T tokens | 5T tokens | 10T tokens |
|---|---|---|---|---|
| 1B | 787 | 1,574 | 3,935 | 7,787 |
| 2B | 1,574 | 3,148 | 7,787 | 15,574 |
GPU days necessary for pre-training
Current state of your GPU

Let’s now look at ways to improve the efficiency of the pre-training.
Efficient pre-training
Two techniques to improve the efficiency and cost of pre-training.
HP transfer
A common practice is to use a small-scale proxy run to tune the hyperparameters. Those hyperparameters can then be zero-shot transferred to the main run, provided that the muP framework is used.

muP vs standard hyperparameter search, from the muP paper
This parametrization stabilizes hyperparameters such as the learning rate and initialization std across different model scales. Other techniques can be found in this compilation of papers about scaling LLM runs, including learning rate/init std and batch size.
This guide presents how to use this parametrization in practice.
Better pre-training with the Muon optimizer
The convergence speed of the pre-training is tightly tied to the optimizer used.
Recent works have used the MUON optimizer because it showed that it could be more efficient than AdamW.

Muon vs AdamW, from Essential AI's paper
The NanoGPT speedrun used this optimizer to reduce the pretraining time by a factor of 1.35x. Those results hold for model up to the GPT2XL scale (1.5B parameters):

Scaling the speedrun to 1.5B models
The largest pre-training runs leveraging this optimizer are from Kimi. Moonlight, a 3B/16B parameters MoE model trained on 5.7T tokens. Kimi K2 release, a 32B/1T parameters MoE model trained on 15.5T tokens, with a modified MuonClip optimizer, specifically designed to avoid loss spikes:
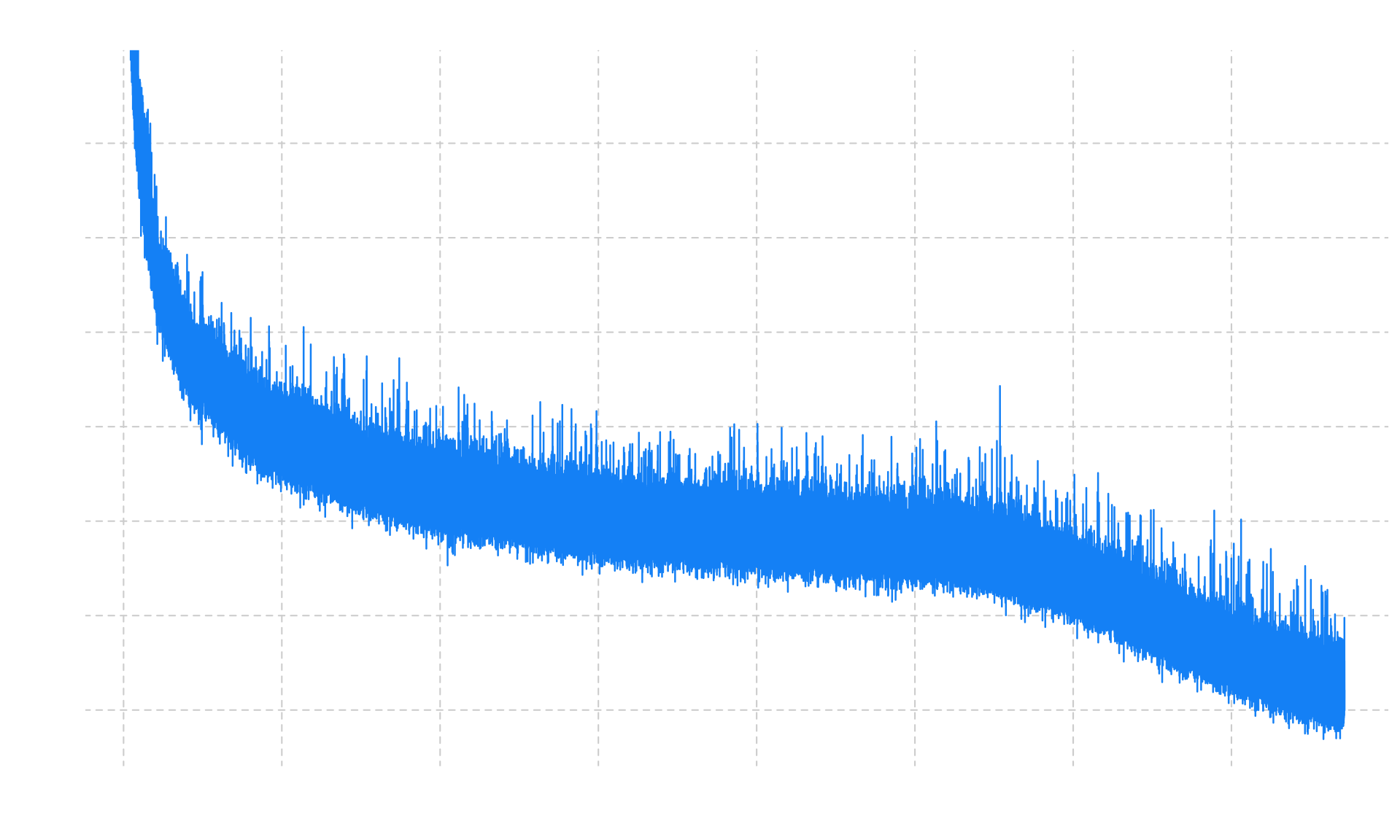
Kimi K2's loss curve, with no loss spikes
A study by Essential AI even combines muP and Muon for better performance, showing a good data efficiency and short training time.
References
- Scaling Laws for Neural Language Models
- Training Compute-Optimal Large Language Models
- PaLM: Scaling Language Modeling with Pathways
- The Ultra-scale Playbook
- muP: Zero-Shot HP Transfer
- What to do to scale up
- The Practitioner's Guide to the Maximal Update Parameterization
- Keller Jordan's blog on Muon
- Practical Efficiency of Muon for Pretraining
- Muon is scalable for LLM training
- Kimi K2 release
Scaling laws
Pre-training and MFU
How to scale
Muon and its Applications
Basic scripts derived from nanoGPT can consistently reach close to 60% MFU on 4 A100 with NVLINK (this is really mandatory for a good MFU), with only data parallelism. In our own experiments, other parallelism schemes, such as tensor parallel, when poorly setup, can be detrimental for MFU, because they require more synchronization. Small models in the 1B range don’t require 2D or 3D parallelism. ↩
The H200 has peak bfloat16 FLOPs between 1,979 TFLOPS and 1,671 TFLOPS according to https://www.nvidia.com/fr-fr/data-center/h200/. The table should be scaled based on the actual hardware used and according to the formula. ↩